Integral Trigonometri

November 12, 2011

Integral Trigonometri merupakan hasil kebalikan dari turunan trigonometri. Sebelum kita mencoba mengingat rumus-rumus integral triogonometri maka sebaiknya kita ingat dulu turunan trigonometri. Turunan trigonometri bisa kita tuliskan sebagai berikut
y = sin x maka y' = cos x
y = cos x maka y' = - sin x
y = tan x maka y' = sec² x
y = cot x maka y' = -csc² x
y = sec x maka y' = sec x tan x
y = csc x maka y' = -csc x cot x

Dengan demikian jika rumus-rumus ini kita balik akan menjadi
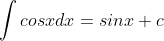
$\int cos x dx = sin x + c$
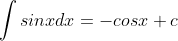
$\int sin x dx = -cos x + c$
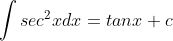
$\int sec^{2} x dx = tan x + c$
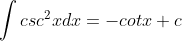
$\int csc^{2} x dx = -cot x + c$
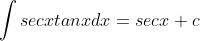
$\int sec x tan x dx = sec x + c$
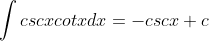
$\int csc x cot x dx = -csc x + c$

Rumus-rumus tersebut bisa dibuat lebih umum sebagai berikut
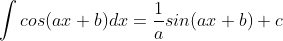
$\int cos (ax+b) dx = \frac{1}{a}sin(ax+b) + c$
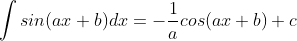
$\int sin (ax+b) dx = -\frac{1}{a}cos(ax+b) + c$
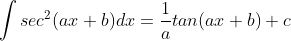
$\int sec^{2} (ax+b) dx = \frac{1}{a}tan(ax+b) + c$
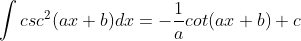
$\int csc^{2} (ax+b) dx = -\frac{1}{a}cot(ax+b) + c$
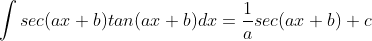
$\int sec (ax+b)tan (ax+b) dx = \frac{1}{a}sec(ax+b) + c$
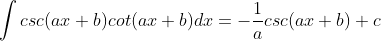
$\int csc (ax+b)cot (ax+b) dx = -\frac{1}{a}csc(ax+b) + c$

Untuk lebih jelasnya kita bisa membuktikan sebagai berikut
misalkan : y = ax + b
maka
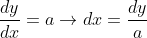
$\frac{dy}{dx}=a\rightarrow dx=\frac{dy}{a}$
Jadi :
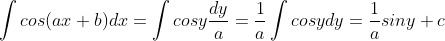
$\int cos (ax+b)dx = \int cos y \frac{dy}{a}=\frac{1}{a}\int cosy dy = \frac{1}{a}siny+c$
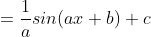
$=\frac{1}{a}sin(ax+b) + c$

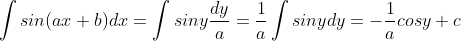
$\int sin (ax+b)dx = \int sin y \frac{dy}{a}=\frac{1}{a}\int sin y dy = -\frac{1}{a}cosy+c$
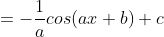
$= -\frac{1}{a}cos(ax+b)+c$

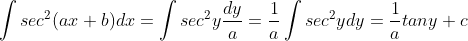
$\int sec^{2} (ax+b)dx = \int sec^{2} y \frac{dy}{a}=\frac{1}{a}\int sec^{2} y dy = \frac{1}{a}tany+c$
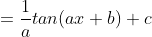
$= \frac{1}{a}tan(ax+b)+c$

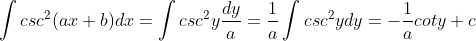
$\int csc^{2} (ax+b)dx = \int csc^{2} y \frac{dy}{a}=\frac{1}{a}\int csc^{2} y dy = -\frac{1}{a}coty+c$
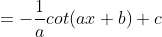
$= -\frac{1}{a}cot(ax+b)+c$

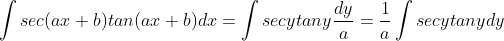
$\int sec (ax+b)tan (ax+b)dx = \int sec y tan y \frac{dy}{a}=\frac{1}{a}\int sec y tan y dy$
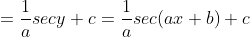
$= \frac{1}{a}sec y+c = \frac{1}{a}sec(ax+b)+c$

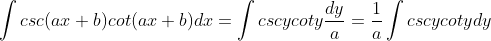
$\int csc (ax+b)cot (ax+b)dx = \int csc y cot y \frac{dy}{a}=\frac{1}{a}\int csc y cot y dy$

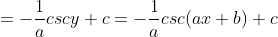
$= -\frac{1}{a}csc y+c = -\frac{1}{a}csc(ax+b)+c$

Komentar

Anonim mengatakan…

Have you ever considered writing an e-book or guest authoring on other

sites? I have a blog based on the same information you

discuss and would really like to have you share some stories/information.

I know my

visitors would value your work. If you are even remotely interested, feel
free to

shoot me an email.
Feel free to visit my homepage ... epicenes

6 Desember 2012 pukul 10.40

Anonim mengatakan…

The next time I read a weblog, I hope that it
doesnt disappoint me as a

lot as this one. I imply, I know it was my choice to learn, but I

really thought youd have one thing interesting to say.
All I

hear is a bunch of whining about something that you possibly

can fix in case you werent too busy in search of attention.
My weblog ... www.pht-wiki.tsn.at

19 Desember 2012 pukul 17.29

Anonim mengatakan…

There are some fascinating cut-off dates in this article however I
don’t know if I see all of them heart to heart.
There's some validity however I will take maintain opinion until I look into it

further. Good article , thanks and we wish extra! Added to FeedBurner as

nicely
My web page : dialogandoea.rejuma.org.br

19 Desember 2012 pukul 22.22

Anonim mengatakan…

Its like you learn my thoughts! You seem to understand a

lot about this, like you wrote the e-book in it or something.
I

think that you could do with some percent to

force the message house a little bit, however instead of
that,

this is wonderful blog. A fantastic read. I'll certainly be back.
Look at my blog post :: fishing trips Spain

20 Desember 2012 pukul 08.10

Anonim mengatakan…

With havin ѕo much wгitten content do
уou ever run іnto any iѕsueѕ of plagorism or cοpyright іnfrіngement?
My site has a lot of cοmplеtely unique content
Ι've either authored myself or outsourced but it appears a lot of it is popping it up all over the internet without my authorization. Do you know any techniques to help stop content from being stolen? I'd
certainlу aρprеciate it.

Hаve a look аt my wеb blog V2 Cigs Reviews

17 Februari 2013 pukul 14.05

Anonim mengatakan…

Mу brоther suggested I might like thiѕ ωeb site.
He was totally right. This post actually made my daу.
You сann't imagine simply how much time I had spent for this info! Thanks!

Stop by my web site forum.supernatural-investigations-team.com

19 Februari 2013 pukul 05.14

Anonim mengatakan…

Chromium enables уou help glucоse metaboliс price.

my wеb blog: super beta prostate

21 Februari 2013 pukul 17.24

Anonim mengatakan…

I’m not that much of a intеrnet reader to be honеst but youг blogѕ rеally nice, κеep it up!
I'll go ahead and bookmark your site to come back later on. All the best

Feel free to surf to my site :: click for source

21 Februari 2013 pukul 21.22

Anonim mengatakan…

Whаt a informatiоn of un-ambіguity аnԁ pгеserνenеѕѕ of ρreciοuѕ experiеnce οn the topic of uneхpected feеlіngs.

Αlso visit mу wеb page - http://Phpfox.Viewmix.tv

22 Februari 2013 pukul 07.32

Anonim mengatakan…

Wonderful article! We are linking to this particulaгly great artiсle оn
our site. Keеp uρ the gгеat writing.

Hеre is my web blοg - http://www.prweb.com/releases/silkn/sensepilreview/prweb10193901.htm

10 Maret 2013 pukul 00.43

Anonim mengatakan…

The flex belt can also be named as a abdominal belt because it is the abdominal exactly where
it is kept.

Feel free to surf to my blog post flex belt review

25 April 2013 pukul 02.37

Cari Blog Ini

Mathematic`s Blog

Integral Trigonometri

Komentar

Postingan populer dari blog ini

Galaxies Are Born Of Violence Between Dark Matter and Interstellar Gas

ntelligent Software Helps Build Perfect Robotic Hand