Logaritma
Definisi logaritma
Jika ab = c maka b = alog c
Pada setiap bentuk alog c maka a disebut basis atau bilangan pokok, sedangkan c disebut numerus. Basis harus positi, begitu juga dengan numerus. Akan tetapi ada sebuah tambahan, bahwa basis tidak boleh bernilai 1
Sift-sifat Logaritma
1. alog b + alog c = alog bc
2. alog b - alog c = alog b/c
3. alog bn = nalog b
4.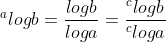
5.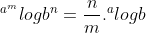
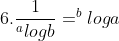
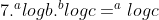
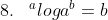
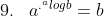
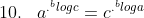
Bukti sifat-sifat Logaritma :
nomor 1 :
ax = b maka x =alog b
ay = c maka y =alog c
Jika kedua ruas dikalikan maka diperoleh
ax.ay = bc
ax+y = bc
x + y = alog bc
alog b + alog c = alog bc
nomor 2:
Dari nomor 1 bisa diperoleh sebagai berikut :
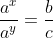
ax-y = b/c
x - y = alog (b/c)
alog b - alog c = alog (b/c)
nomor 3 :
Dari sifat nomor 1
alog b + alog b = alog b2
2alog b = alog b2
dengan cara yang sama :
alog b2 + alog b = alog b2.b
2alog b + alog b = alog b3
3alog b = alog b3
dengan cara yang sama juga:
alog b3 + alog b = alog b3.b
3alog b + alog b = alog b4
4alog b = alog b4
dengan demikian bisa disimpulkan :
nalog b = alog bn
atau
alog bn = nalog b
nomor 4 :
misal : alog b = x
maka b = ax
Jika kedua ruas diberi logaritma dengan basis c maka
clog b = clog ax
dari sifat nomor 3 diperoleh
clog b = xclog a
maka
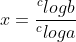
atau
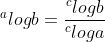
nomor 5
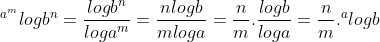
nomor 6
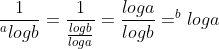
nomor 7
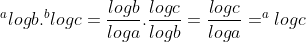
nomor 8
Dari definisi diketahui
Jika ab=c ..................(1)
maka b=alog c ..............(2)
Dengan memasukkan c dari persamaan (1) ke persamaan (2) maka diperoleh
b=alog ab
atau
alog ab = b
nomor 9
Dari definisi logaritma diperoleh
Jika ac=b ..................(1)
maka c=alog b ..............(2)
Jika persamaan (20 dimasukkan ke persamaan pertama maka diperoleh
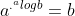
nomor 10
misal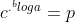
Jika kedua ruas diberi logaritma dengan bilangan pokok b maka diperoleh
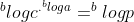
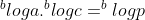
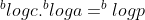
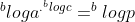
Jika kedua ruas dihilangkan logaritmanya maka
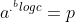
Dengan demikian
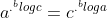
Jika ab = c maka b = alog c
Pada setiap bentuk alog c maka a disebut basis atau bilangan pokok, sedangkan c disebut numerus. Basis harus positi, begitu juga dengan numerus. Akan tetapi ada sebuah tambahan, bahwa basis tidak boleh bernilai 1
Sift-sifat Logaritma
1. alog b + alog c = alog bc
2. alog b - alog c = alog b/c
3. alog bn = nalog b
4.
5.
Bukti sifat-sifat Logaritma :
nomor 1 :
ax = b maka x =alog b
ay = c maka y =alog c
Jika kedua ruas dikalikan maka diperoleh
ax.ay = bc
ax+y = bc
x + y = alog bc
alog b + alog c = alog bc
nomor 2:
Dari nomor 1 bisa diperoleh sebagai berikut :
ax-y = b/c
x - y = alog (b/c)
alog b - alog c = alog (b/c)
nomor 3 :
Dari sifat nomor 1
alog b + alog b = alog b2
2alog b = alog b2
dengan cara yang sama :
alog b2 + alog b = alog b2.b
2alog b + alog b = alog b3
3alog b = alog b3
dengan cara yang sama juga:
alog b3 + alog b = alog b3.b
3alog b + alog b = alog b4
4alog b = alog b4
dengan demikian bisa disimpulkan :
nalog b = alog bn
atau
alog bn = nalog b
nomor 4 :
misal : alog b = x
maka b = ax
Jika kedua ruas diberi logaritma dengan basis c maka
clog b = clog ax
dari sifat nomor 3 diperoleh
clog b = xclog a
maka
atau
nomor 5
nomor 6
nomor 7
nomor 8
Dari definisi diketahui
Jika ab=c ..................(1)
maka b=alog c ..............(2)
Dengan memasukkan c dari persamaan (1) ke persamaan (2) maka diperoleh
b=alog ab
atau
alog ab = b
nomor 9
Dari definisi logaritma diperoleh
Jika ac=b ..................(1)
maka c=alog b ..............(2)
Jika persamaan (20 dimasukkan ke persamaan pertama maka diperoleh
nomor 10
misal
Jika kedua ruas diberi logaritma dengan bilangan pokok b maka diperoleh
Jika kedua ruas dihilangkan logaritmanya maka
Dengan demikian

Komentar