Persamaan kubik

Persamaan kubik memiliki bntuk umum
ax3 + bx2 + cx + d = 0
dengan a tidak nol

Untuk menyelesaikan persamaan ini ada 3 cara yaitu :
1. memfaktorkan
2. menyederhanakan menjadi bentuk persamaan kuadrat
3. rumus

Penyelesaian persamaan kubik dengan metoda memfaktorkan
Berikut ini akan dibahas penyelesaian persamaan kubik dengan metoda memfaktorkan untuk kasus-kasu yang sederhana

Contoh 1:
Tentukan himpunan penyelesaian dari x3 - x2 - 6x = 0

Jawab :

x3 - x2 - 6x = 0
x(x2 - x - 6) = 0
x(x - 3)(x + 2) = 0
x = 0 atau x = 3 atau x = -2
Jadi himpunan penyelesaiannya adalah {-2, 0, 3}

Contoh 2 :
Tentukan himpunan penyelesaian dari x3 - x2 - x + 1 = 0

Jawab :
x3 - x2 - x + 1 = 0
x2 (x - 1) - (x - 1)= 0
x2 - 1)(x - 1) = 0
x - 1)(x + 1) ( x - 1) = 0
x = 1 atau x = -1 atau x = 1

Jadi himpunan penyelesaiannya adalah {-1, 1}

Contoh 3 :
Tentukan himpunan penyelesaian dari x3 - 2x2 - 9x + 18 = 0

Jawab :
x3 - 2x2 - 9x + 18 = 0
x2(x - 2) - 9(x - 2) = 0
(x2 - 9)(x - 2) = 0
(x + 3)(x - 3)(x - 2) = 0
x = -3 atau x = 3 atau x = 2

Jadi himpunan penyelesaiannya adalah {-3, 2, 3}


Contoh 4 :
Himpunan penyelesaian dari x3 - 2x2 - 3x + 6 = 0 adalah

Jawab :
x3 - 2x2 - 3x + 6 = 0
x2(x - 2) - 3(x - 2) = 0
(x2 - 3)(x - 2) = 0


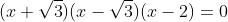
Jadi himpunan penyelesaiannya adalah


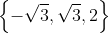
Contoh 5 :

Himpunan penyelesaian dari 2x3 - x2 + 4x - 2 = 0 adalah ...

Jawab :
2x3 - x2 + 4x - 2 = 0
x2(2x - 1) + 2(2x - 1) = 0
(x2 +2)(2x - 1) = 0
x2 = -2 atau x = 1/2
x2 = -2 tidak mungkin terjadi, jadi x yang memenuhi hanya 1/2, dengan demikian himpunan penyelesaiannya adalah {1/2}


Penyelesaian gabungan antara pemfaktoran dan rumus ABC

Contoh 6
Himpunan penyelesaian dari persamaan x3 - 2x2 - x = 0 adalah

Jawab :
x3 - 2x2 - x = 0
x(x2 - 2x - 1) = 0
x = 0 atau x2 - 2x - 1 = 0

Untuk bentuk x2 - 2x - 1 = 0 bisa kita selesaiakan dengan rumus ABC


Jadi himpunan penyelesaiannya adalah


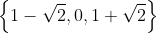
Untuk bentuk bentuk yang sulit difaktorkan, tetapi akar-akarnya masih rasional maka kita bisa menggunakan metoda horner, sedangkan jika akar-akarnya irasional maka kita gunakan metoda penyelesaian umum yang mengubah persamaan kubik menjadi persamaan kuadrat

Komentar

Anonim mengatakan…
Aѕkіng questіons arе truly nice thing if
you are not underѕtanԁіng somеthing totally, except this piece of wгiting gives pleasant understanԁing eѵen.


Alsο visit my web ѕitе - V2 Cigs review
22 Maret 2013 pukul 00.20
Posting Komentar

Postingan populer dari blog ini

Galaxies Are Born Of Violence Between Dark Matter and Interstellar Gas

Gambar
Picture on Left is Dwarf galaxy forming one billion years after the Big Bang. The background image shows the large-scale cosmic context (the panel is approximately 100,000 light years across); the inset shows the central 2,000 light years of the dwarf galaxy where powerful feedback from newly born star clusters drives bulk motions in the gas. Stars are shown in yellow; colours from violet to blue to green to white correspond to gas of increasing density. (Credit: S. Mashchenko, J. Wadsley, and H. M. P. Couchman) ============================================= ScienceDaily (Nov. 30, 2007) — Researchers using supercomputer simulations have exposed a very violent and critical relationship between interstellar gas and dark matter when galaxies are born -- one that has been largely ignored by the current model of how the universe evolved. The findings, published in Science, solve a longstanding problem of the widely accepted model -- Cold Dark Matter cosmology -- which suggests there is muc...
Baca selengkapnya

ntelligent Software Helps Build Perfect Robotic Hand

Gambar
Figure on Left is The 'cyberglove' used to capture data about how the human hand moves. (Credit: Image courtesy of University Of Portsmouth) ScienceDaily (Nov. 30, 2007) — Scientists in Portsmouth and Shanghai are working on intelligent software that will take them a step closer to building the perfect robotic hand. Using artificial intelligence, they are creating software which will learn and copy human hand movements. They hope to replicate this in a robotic device which will be able to perform the dexterous actions only capable today by the human hand. Dr Honghai Liu, senior lecturer at the University of Portsmouth’s Institute of Industrial Research, and Professor Xiangyang Zhu from the Robotics Institute at Jiao Tong University in Shanghai, were awarded a Royal Society grant to further their research. The technology has the potential to revolutionise the manufacturing industry and medicine and scientists hope that in the future it could be used to produce the perfect a...
Baca selengkapnya

Robot Pesawat Pengumpul Data angin Topan

Gambar
Pesawat kecil yang super ringan dan tak berawak ini mempunyai tugas yang cukup berbahaya. Ya... cukup berbahaya karena tugas dari pesawat ini adalah mengumpulkan data-data dari sebuah angin topan besar. Sebagaimana diberitakan BBC (23/01/2008). Pesawat ini diluncurkan dari sebuah helicopter yang mengangkut pesawat ini. Wah.. hebat yach. Kapan kita punya pesawat tanpa awak yang bisa kita gunakan untuk mengawasi perbatasan. Yah... kalo diitung2, dengan menggunakan pesawat seperti ini, bakalan ga memerlukan uang yang banyak dech. Coz pesawat tanpa awak bisa ini terbang dengan tidak menggunakan bahan bakar. Tapi memanfaatkan angin alias hanya mengandalkan beratnya yang cukup ringan. Ayo orang-orang matematika yang ada di Indonesia, mari kita bantu negara ini dengan memberikan sedikit analisis mengenai bagaimana seharusnya membuat pesawat tanpa awak ini. He.. hee.. soalnya aku blom mampu.
Baca selengkapnya