Turunan 3
Contoh 4 :
Turunan pertama dari
![\fn_jvn f(x)=\sqrt[3]{x}](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%28x%29=%5Csqrt[3]%7Bx%7D)
adalah
Jawab :
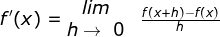
![\fn_jvn f'(x)=\begin{matrix} lim\\h \to \0 \end{matrix}\frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h}](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%27%28x%29=%5Cbegin%7Bmatrix%7D%20lim%5C%5Ch%20%5Cto%20%5C0%20%5Cend%7Bmatrix%7D%5Cfrac%7B%5Csqrt[3]%7Bx+h%7D-%5Csqrt[3]%7Bx%7D%7D%7Bh%7D)
![\fn_jvn f'(x)=\begin{matrix} lim\\h \to \0 \end{matrix}\left ( \frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h} \right )\left ( \frac{\sqrt[3]{(x+h)^{2}}+\sqrt[3]{(x+h)x}+\sqrt[3]{x^{2}}}{\sqrt[3]{(x+h)^{2}}+\sqrt[3]{(x+h)x}+\sqrt[3]{x^{2}}} \right )](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%27%28x%29=%5Cbegin%7Bmatrix%7D%20lim%5C%5Ch%20%5Cto%20%5C0%20%5Cend%7Bmatrix%7D%5Cleft%20%28%20%5Cfrac%7B%5Csqrt[3]%7Bx+h%7D-%5Csqrt[3]%7Bx%7D%7D%7Bh%7D%20%5Cright%20%29%5Cleft%20%28%20%5Cfrac%7B%5Csqrt[3]%7B%28x+h%29%5E%7B2%7D%7D+%5Csqrt[3]%7B%28x+h%29x%7D+%5Csqrt[3]%7Bx%5E%7B2%7D%7D%7D%7B%5Csqrt[3]%7B%28x+h%29%5E%7B2%7D%7D+%5Csqrt[3]%7B%28x+h%29x%7D+%5Csqrt[3]%7Bx%5E%7B2%7D%7D%7D%20%5Cright%20%29)
![\fn_jvn f'(x)=\begin{matrix} lim\\h \to \0 \end{matrix}\left \frac{x+h-x}{h\left ( \sqrt[3]{(x+h)^{2}}+\sqrt[3]{(x+h)x}+\sqrt[3]{x^{2}} \right )}](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%27%28x%29=%5Cbegin%7Bmatrix%7D%20lim%5C%5Ch%20%5Cto%20%5C0%20%5Cend%7Bmatrix%7D%5Cleft%20%5Cfrac%7Bx+h-x%7D%7Bh%5Cleft%20%28%20%5Csqrt[3]%7B%28x+h%29%5E%7B2%7D%7D+%5Csqrt[3]%7B%28x+h%29x%7D+%5Csqrt[3]%7Bx%5E%7B2%7D%7D%20%5Cright%20%29%7D)
![\fn_jvn f'(x)=\begin{matrix} lim\\h \to \0 \end{matrix}\left \frac{h}{h\left ( \sqrt[3]{(x+h)^{2}}+\sqrt[3]{(x+h)x}+\sqrt[3]{x^{2}} \right )}](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%27%28x%29=%5Cbegin%7Bmatrix%7D%20lim%5C%5Ch%20%5Cto%20%5C0%20%5Cend%7Bmatrix%7D%5Cleft%20%5Cfrac%7Bh%7D%7Bh%5Cleft%20%28%20%5Csqrt[3]%7B%28x+h%29%5E%7B2%7D%7D+%5Csqrt[3]%7B%28x+h%29x%7D+%5Csqrt[3]%7Bx%5E%7B2%7D%7D%20%5Cright%20%29%7D)
![\fn_jvn f'(x)=\begin{matrix} lim\\h \to \0 \end{matrix}\left \frac{1}{\sqrt[3]{(x+h)^{2}}+\sqrt[3]{(x+h)x}+\sqrt[3]{x^{2}}}](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%27%28x%29=%5Cbegin%7Bmatrix%7D%20lim%5C%5Ch%20%5Cto%20%5C0%20%5Cend%7Bmatrix%7D%5Cleft%20%5Cfrac%7B1%7D%7B%5Csqrt[3]%7B%28x+h%29%5E%7B2%7D%7D+%5Csqrt[3]%7B%28x+h%29x%7D+%5Csqrt[3]%7Bx%5E%7B2%7D%7D%7D)
![\fn_jvn f'(x)=\frac{1}{\sqrt[3]{(x+0)^{2}}+\sqrt[3]{(x+0)x}+\sqrt[3]{x^{2}}}](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%27%28x%29=%5Cfrac%7B1%7D%7B%5Csqrt[3]%7B%28x+0%29%5E%7B2%7D%7D+%5Csqrt[3]%7B%28x+0%29x%7D+%5Csqrt[3]%7Bx%5E%7B2%7D%7D%7D)
![\fn_jvn f'(x)=\frac{1}{3\sqrt[3]{x^{2}}}](http://latex.codecogs.com/gif.latex?%5Cfn_jvn%20f%27%28x%29=%5Cfrac%7B1%7D%7B3%5Csqrt[3]%7Bx%5E%7B2%7D%7D%7D)
contoh 5
Tetukan turunan pertama dari f(x) = sin x
Jawab :
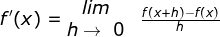
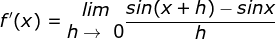
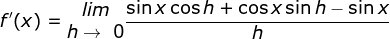
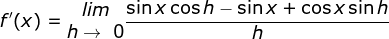
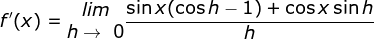
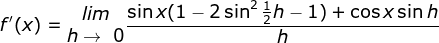
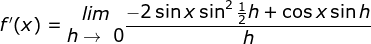
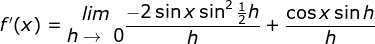
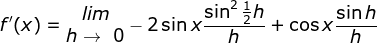
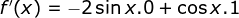
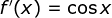
Cara II :
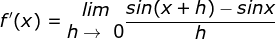
Dengan memakai rumus
maka diperoleh
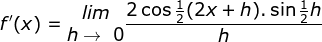
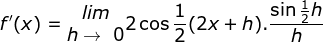
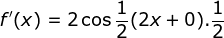
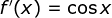
Turunan pertama dari
adalah
Jawab :
contoh 5
Tetukan turunan pertama dari f(x) = sin x
Jawab :
Cara II :
Dengan memakai rumus
sin A – sin B = 2 cos ½ (A + B) sin ½ (A – B)

Komentar
Merkur Progress Adjustable Safety Razor, Barber Pole, Black (9" 1xbet X deccasino 5.4" หารายได้เสริม - 9 inches) | DE Safety Razor, Merkur Progress Double Edge Safety Razor, Futur 700, Safety Razor,